Rectas y parábolas
Contenido de esta página:
- Recordatorio de rectas y parábolas
- 10 problemas resueltos sobre rectas
- 10 problemas resueltos sobre parábolas
1. Rectas
La ecuación general de una recta es
Ejemplo: la pendiente de la recta es y la ordenada es .
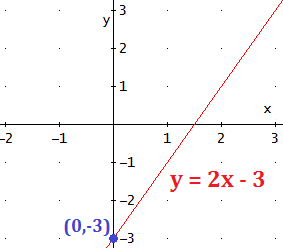 Observando su gráfica:
Observando su gráfica:
Ocurre cuando .
Para calcular el punto, resolvemos la ecuación que resulta al cambiar por 0. Es decir, resolvemos la ecuación de primer grado
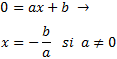
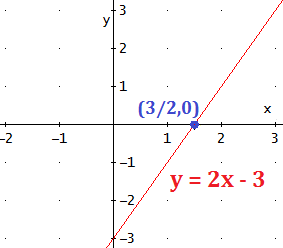 Con el eje OY (de ordenadas)
Con el eje OY (de ordenadas)
Ocurre cuando .
Para calcular el punto, calculamos sustituyendo por 0 en la ecuación. Obtendremos la ordenada: .
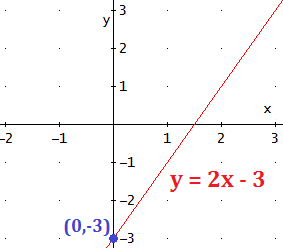
Recta horizontal:
Una recta es horizontal cuando su pendiente es 0. Por tanto, su ecuación es de la forma
Una recta horizontal es paralela al eje OX y, por tanto, nunca corta a dicho eje (excepto cuando ).
Ejemplos: las rectas e son rectas horizontales:
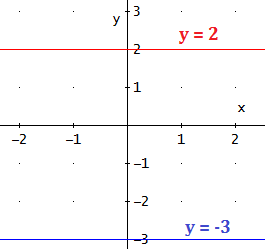 Recta vertical:
Recta vertical:
La ecuación general de una recta vertical es
Ejemplos: las rectas y son rectas vertivales:
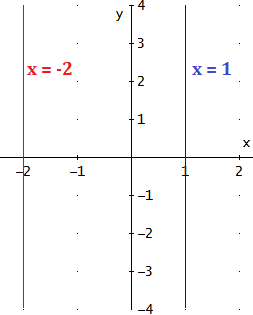
Al número se le llama pendiente y al número , término independiente u ordenada al origen.
Ejemplo: la pendiente de la recta es y la ordenada es .
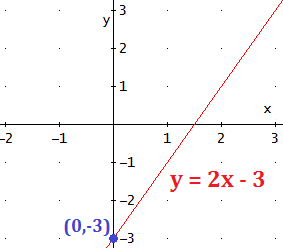
- La recta es creciente (de izquierda a derecha) porque su pendiente es positiva.
- La recta corta al eje OY en el punto ) porque su ordenada es .
Puntos de corte con los ejes
Con el eje OX (de abscisas)Ocurre cuando .
Para calcular el punto, resolvemos la ecuación que resulta al cambiar por 0. Es decir, resolvemos la ecuación de primer grado
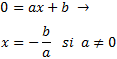
El punto de corte de la recta con el eje OX es .
Ejemplo: el punto de corte de la recta con el eje OX es :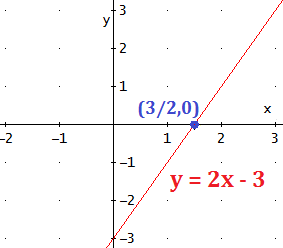
Ocurre cuando .
Para calcular el punto, calculamos sustituyendo por 0 en la ecuación. Obtendremos la ordenada: .
El punto de corte de la recta con eje eje OY es .
Ejemplo: el punto de corte con el eje OY de la recta es :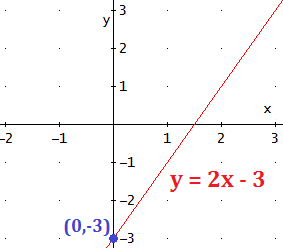
Rectas especiales
Hay dos tipos de rectas que consideramos especiales: las rectas horizontales y las rectas verticales.Recta horizontal:
Una recta es horizontal cuando su pendiente es 0. Por tanto, su ecuación es de la forma
La recta corta al eje OY en el punto y si , entonces coincide con el eje OX.
Una recta horizontal es paralela al eje OX y, por tanto, nunca corta a dicho eje (excepto cuando ).
Ejemplos: las rectas e son rectas horizontales:
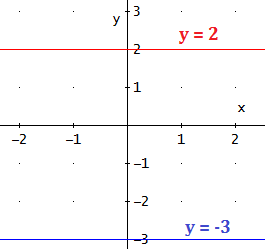
La ecuación general de una recta vertical es
Esta recta corta el eje OX en el punto y si , entonces la recta coincide con el eje OY.
Una recta vertical no tiene pendiente ni ordenada.
Nota: una recta vertical no es la gráfica de una función. Por ello, en su ecuación no aparece la .Ejemplos: las rectas y son rectas vertivales:
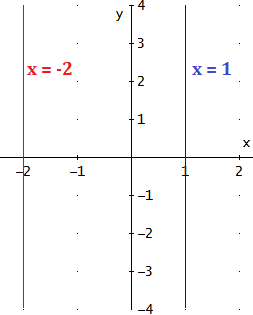
2. Parábolas
El coeficiente se denomina coeficiente principal y el coeficiente , término independiente.
Forma de una parábola
El coeficiente de la parábola determina su orientación.- Cuando , la parábola tiene forma de U. Por ejemplo,
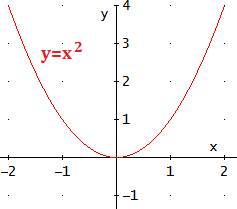
- Cuando , tiene forma de U invertida. Por ejemplo,
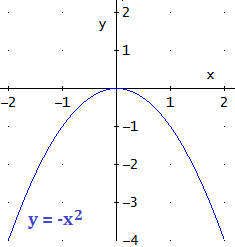
Puntos de corte con los ejes
Con el eje OX (de abscisas)Ocurre cuando .
Para calcular el punto, resolvemos la ecuación que resulta al cambiar por 0. Es decir, resolvemos la ecuación de segundo grado
Ejemplos:
- La parábola tiene sólo un punto de corte con OX:
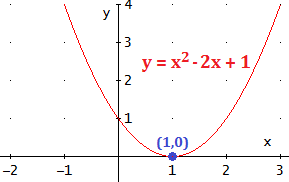
- La parábola tiene dos puntos de corte con OX:
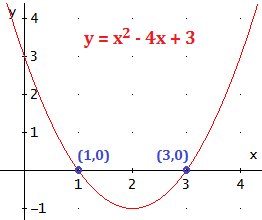
- La parábola no tiene puntos de corte con OX:
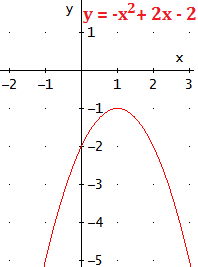
Ocurre cuando .
Para calcular el punto, calculamos sustituyendo por 0 en la ecuación. Obtendremos y, por tanto, el punto de corte con OY es .
Vértice de una parábola
El vértice de una parábola está en el punto cuya primera coordenada esSi la parábola tiene forma de U, el vértice es un mínimo. Si tiene forma de U invertida, es un máximo.
El vértice está en el punto cuya primera coordenada es
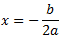
Ejemplos:
- El vértice de la parábola es un máximo:
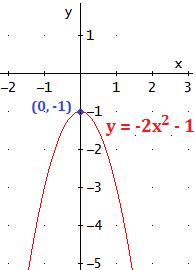
- El vértice de la parábola es un mínimo:
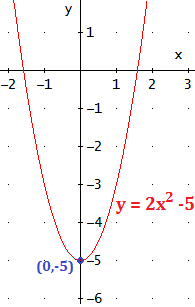
3. Problemas sobre rectas
Problema 1
Calcular los puntos de corte de los ejes con la recta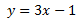
¿El punto A(1, 2) es un punto de la recta?
Solución
Problema 2
Calcular los puntos de corte de los ejes con la recta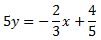
¿El punto A(1, 2) es un punto de la recta?
Solución
Problema 3
Calcular los puntos de corte de los ejes con la recta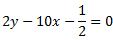
¿El punto A(2, 10.25) es un punto de la recta?
Solución
Problema 4
Calcular la ecuación de una recta que pase por los puntos A(-3,2) y B(-2,3).¿Cuántas rectas hay que pasen por los puntos A y B?
Solución
Problema 5
Calcular la recta que pasa por el punto A(7,7) y que tiene pendiente -3. ¿Pasa también por el origen?Nota: el origen es el punto O(0,0).
Solución
Problema 6
Responder las siguientes cuestiones:- ¿Cuántas rectas diferentes hay que pasen por dos puntos distintos A y B?
- ¿Cómo podemos saber si una recta pasa por un punto P(m, n)?
- ¿Cuál es la pendiente de una recta horizontal (paralela al eje OX)?
- Dos rectas (distintas) que no se cortan son rectas paralelas. Las siguientes dos rectas son paralelas:
Observando sus ecuaciones, ¿cómo podemos deducir que son paralelas?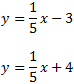
Dar ejemplos de otras rectas paralelas a las anteriores. - Dada una recta, ¿cuántas rectas (distintas) son paralelas a dicha recta?
Solución
Problema 7
Las siguientes rectas no son paralelas y, por tanto, se cortan en un punto. Calcular dicho punto: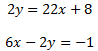
Solución
Problema 8
Las gráficas de las siguientes rectas se cortan en los vértices de un triángulo. Escribir los puntos de los vértices y calcular la longitud de la base del triángulo: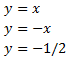
Solución
Problema 9
Encontrar, si existen:- la recta que une los tres puntos A(-1, -15), B(3, 9) y C(2, 3);
- la recta que une los tres puntos D(0,9), E(-2, 21) y F(8, 0).
Solución
No hay comentarios:
Publicar un comentario